1.2 Logistic Regression as a Neural Network

1.2.1 Binary Classification

Binary classification is the task of classifying the elements of a given set into two groups (predicting which group each one belongs to) on the basis of a classification rule.

摘自 wikipedia

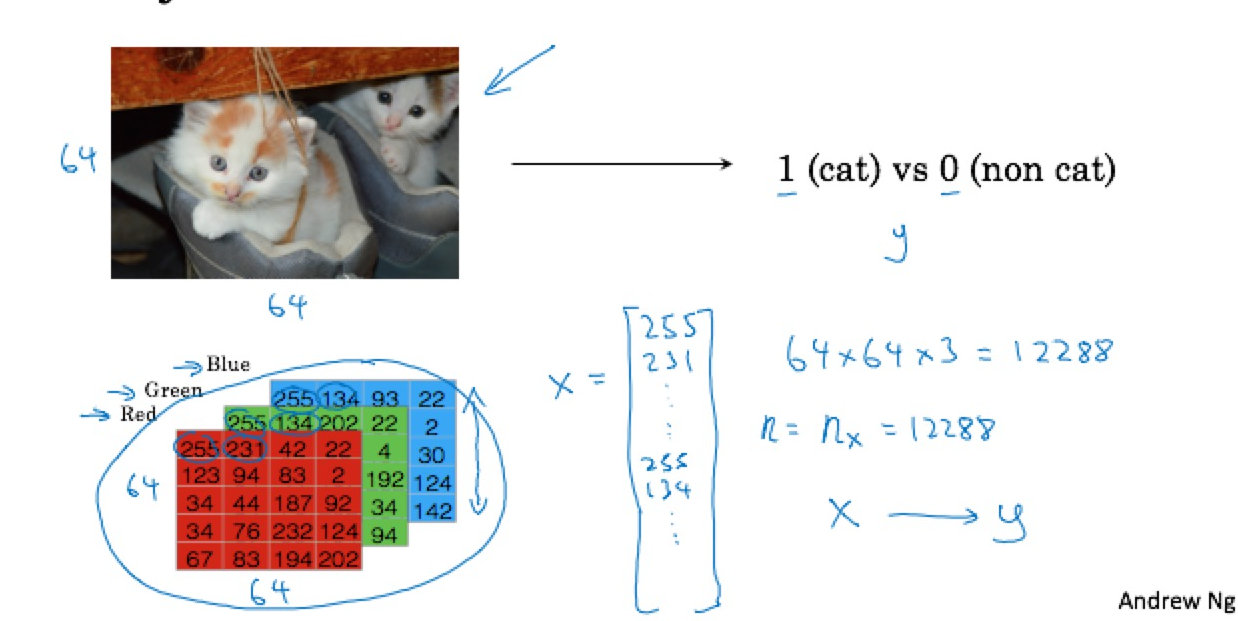
2. Logistic Regression

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships among variables. -- wikipedia

Logistic regression is a learning algorithm used in a supervised learning problem when the output 𝑦 are all either zero or one. The goal of logistic regression is to minimize the error between its predictions and training data. -- Andrew NG

In linear regression we tried to predict the value of $y^{(i)}$ for the $i$‘th example $x^{(i)}$ using a linear function $y = h_\theta(x) = \theta^\top x.$. This is clearly not a great solution for predicting binary-valued labels $\left(y^{(i)} \in\{0,1\}\right)$. In logistic regression we use a different hypothesis class to try to predict the probability that a given example belongs to the “1” class versus the probability that it belongs to the “0” class.

$$\begin{align} P(y=1|x) &= h_\theta(x) = \frac{1}{1 + \exp(-\theta^\top x)} \equiv \sigma(\theta^\top x),\\ P(y=0|x) &= 1 - P(y=1|x) = 1 - h_\theta(x). \end{align}$$

总结：

• is a regression model where the dependent variable (DV) is categorical.

• 一般指case of a binary dependent variable where the output can take only two values, "0" and "1".Cases where the dependent variable has more than two outcome categories may be analysed in multinomial logistic regression(known by softmax regression).

• uses the logistic function(sigmoid function). $S(\theta) = 1/(1+e^{-\theta})$

3. Logistic Regression Cost Function

补充：

• 不能用squared error $L(y, y') = {(y' - y)^2}/2$做loss (error) function，不然optimization problem will becomes not convex，So you end up with optimization problem with multiple local optima. So gradient descent may not find the global optimum

4. Gradient Descent

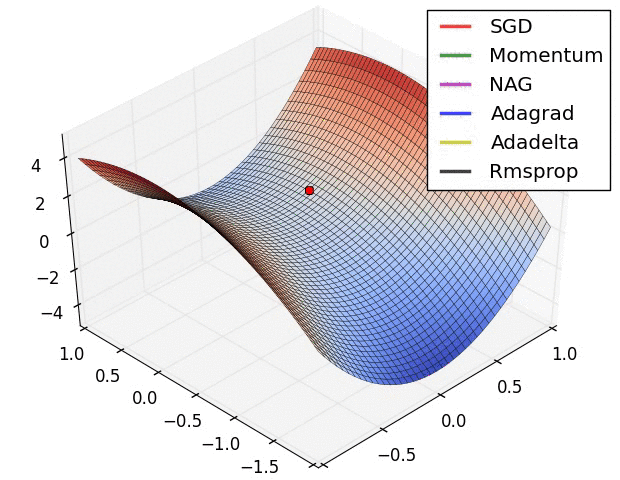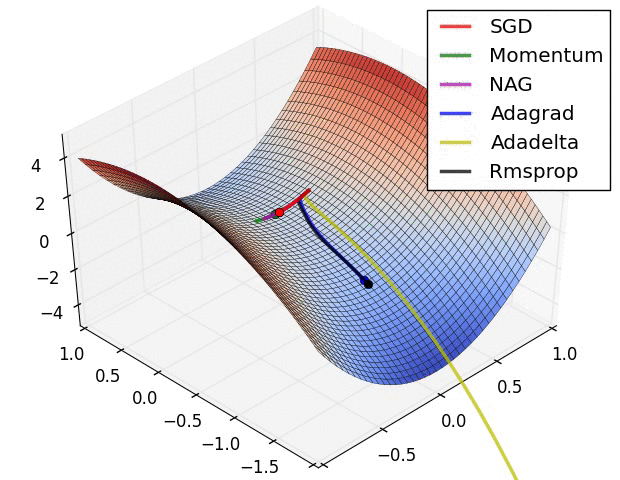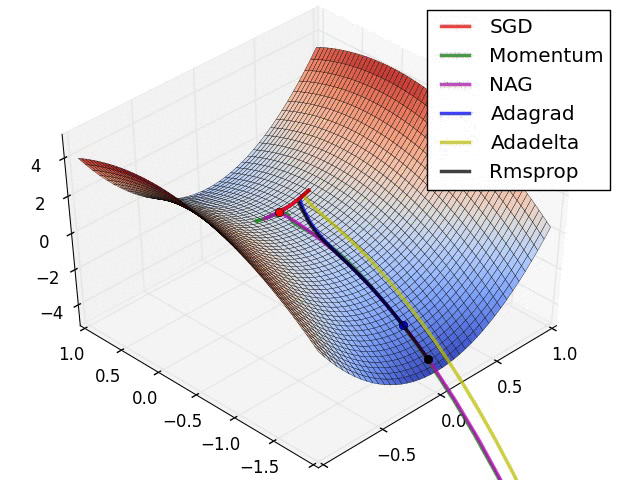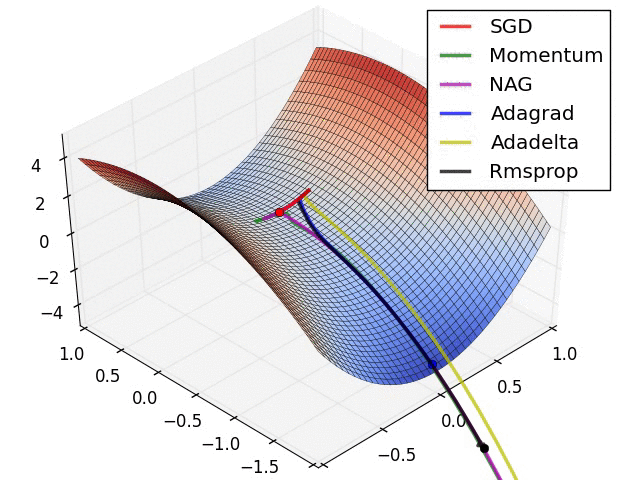
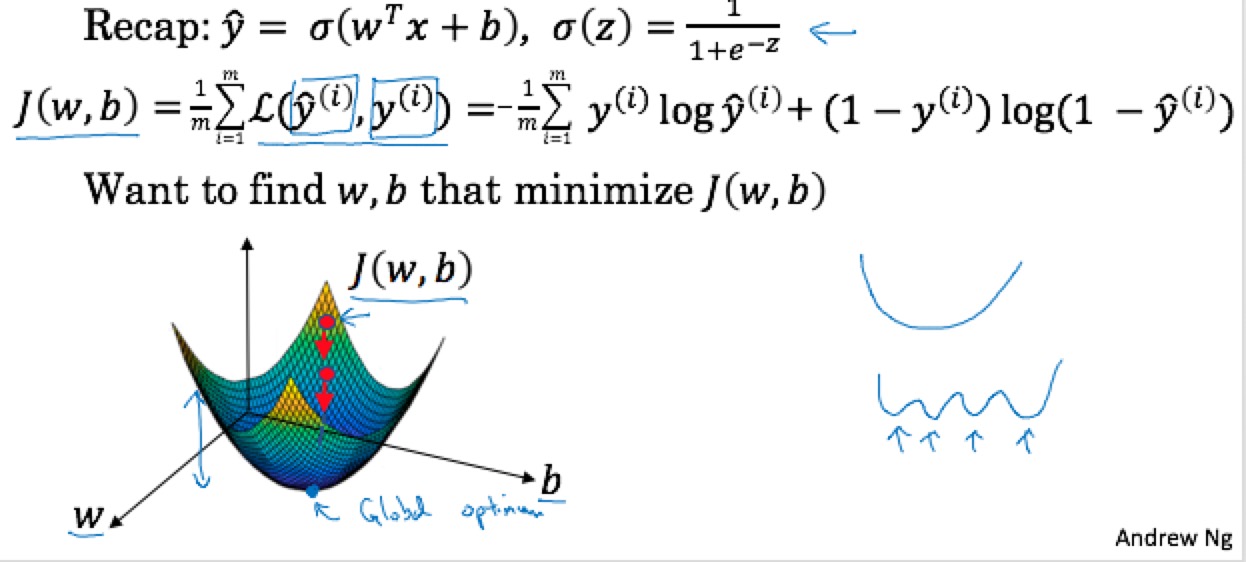
Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function. -- wikipedia

# Vanilla version of Gradient Descent
## This simple loop is the core idea of Gradient Decent. 

while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += - step_size * weights_grad # perform parameter update

Intuition for Gradient Descent:

• A random position on the surface of the bowl is the cost of the current values of the weights (cost).

• The bottom of the bowl is the cost of the best set of weights, the minimum of the function.

• The goal is to continue to try different values for the weights, evaluate their cost and select new weights that have a slightly better (lower) cost.

• Repeating this process enough times will lead to the bottom of the bowl and you will know the values of the weights that result in the minimum cost.

$W_{n+1} = W_n - step\_size * \left. \frac{\partial J(w, b)}{\partial w}\right|_{w=W_n}$

5. Derivatives

{

$\theta$: weights, $x^i$: i'th input(example), $b$: bias

}

$$\theta x^i:=\theta_0+\theta_1 x^i_1+\dots+\theta_p x^i_p. (1)$$ then

$$\log h_\theta(x^i)=\log\frac{1}{1+e^{-\theta x^i} }=-\log ( 1+e^{-\theta x^i} ), (2)$$

$$\log(1- h_\theta(x^i))=\log(1-\frac{1}{1+e^{-\theta x^i} })=\log (e^{-\theta x^i} )-\log ( 1+e^{-\theta x^i} )=-\theta x^i-\log ( 1+e^{-\theta x^i} ), (3)$$

[ this used: $1 = \frac{(1+e^{-\theta x^i})}{(1+e^{-\theta x^i})}$, the 1's in numerator cancel, then we used: $\log(x/y) = \log(x) - \log(y)$ ]

cost function is the form of:

$$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}y^{i}\log(h_\theta(x^{i}))+(1-y^{i})\log(1-h_\theta(x^{i})) (4)$$

Plugging (2) and (3) into (4), we obtain:

$$J(\theta)=-\frac{1}{m}\sum_{i=1}^m \left[-y^i(\log ( 1+e^{-\theta x^i})) + (1-y^i)(-\theta x^i-\log ( 1+e^{-\theta x^i} ))\right] (5)$$

simplified to:

$$J(\theta)=-\frac{1}{m}\sum_{i=1}^m \left[y_i\theta x^i-\theta x^i-\log(1+e^{-\theta x^i})\right]=-\frac{1}{m}\sum_{i=1}^m \left[y_i\theta x^i-\log(1+e^{\theta x^i})\right], (6)$$

where the second equality follows from:

$$-\theta x^i-\log(1+e^{-\theta x^i})= -\left[ \log e^{\theta x^i}+ \log(1+e^{-\theta x^i} ) \right]=-\log(1+e^{\theta x^i}).$$

[ we used $log(x)+log(y)=log(xy)$]

All you need now is to compute the partial derivatives of (5). As

$$\frac{\partial}{\partial \theta_j}y_i\theta x^i=y_ix^i_j,$$

$$\frac{\partial}{\partial \theta_j}\log(1+e^{\theta x^i})=\frac{x^i_je^{\theta x^i}}{1+e^{\theta x^i}}=x^i_jh_\theta(x^i),$$

6. More Derivative Examples

7. Computation graph

8. Derivatives with a Computation Graph

9. Logistic Regression Gradient Descent

10. Gradient Descent on m Examples